gaz-sensor/hardware/README.md

Hardware

LTSpice Simulation

Impédence du capteur de gaz : plusieurs gigaohms -> il faut donc amplifier le signal.

En amplifiant on amplifie aussie le bruit ! Il faut donc filtrer :

1. Filtrer le bruit hf de mesure
2. Fitlrer le bruit 50Hz
3. Filtrer l'échantillonnage de l'ADC

Ampli normal avec gros offset

Ampli LT1050 très faible offset

Schéma ampli + filtres (en bleu)

Fréquence de coupure du premier filtre : 16Hz

Fréquence de coupure du deuxième filtre : 1.5Hz

Fréquenc de coupure du troisième filtre : 1.6kHz

Atténuation à :

• 50Hz : 40db
• Fréquence de Shannon Nyquist (2fmax adc 15kHz) : 108dB

Simulation avec modèle du capteur de gaz

V = RI <=> I = 1/R V <=> I = V * G (Conductance en Siemens)

Modèle du capteur de gaz : I=V(cp,cn)*(10n+(v(gc,gn)*10n))

t=0: V(cp,cn)=0 I=V(cp,cn)*(10nS)

Si t>>1: V(gc,gn)=1 I=V(cp,cn)*(10nS+10mS)

tau=R0*C0

Buit 50Hz atténué

Bruit 50Hz non atténué

Calcul de la résistance totale du schéma :

On est a basse fréquence donc les capacités sont analogues à des circuits ouverts, on a alors une succéssion de ponts diviseurs :

Rsortie = (1+R3/R)R1Vcc/Vadc - R1 - R5

On peut brancher un potentiomètre numérique pour faire varier l'amplification et éviter de saturer dynamiquement.

Calculating R_{cal1} to the best settings possible

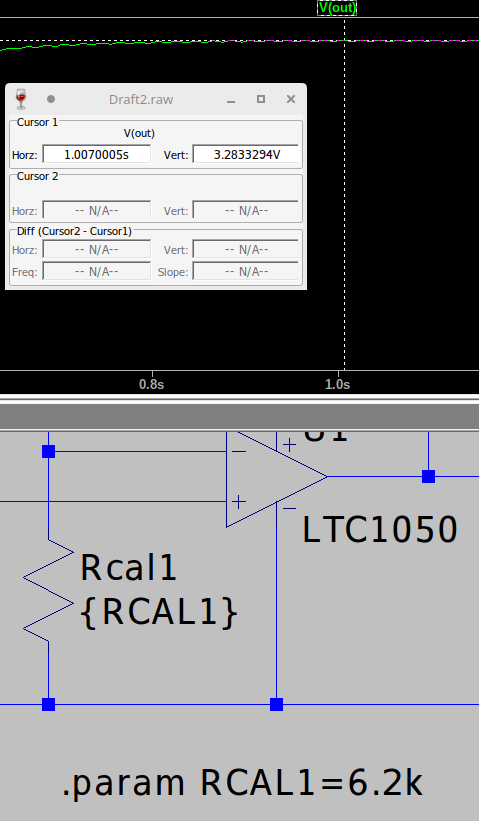
By modifying the R_{cal1} resistor we can see that the maximum output voltage can go up to 5V. The goal would be to modify this resistor value to have a maximum output of around 3.3V:

Calculate a

a=\frac{\Delta{y}}{\Delta{x}}=\frac{y_2-y_1}{x_2-x_1}

AN: a=\frac{10k-1k}{2.1-4.94}

AN: a=-3170

Calculate b

y=-3170x+b

1000=-3170(4.94)+b

b=3170(4.94)+1000

b=16659

Numerical Application

y=-3170x+16659

We can now calculate the resistor R_{cal1} to have 3.3V in maximum output with the previous formula, we find:

-3.17\times{10^3\times{3.3V}}+16.7\times{10^3}=6.2k\Omega

Has we can see with the LTSpice simulation, we have the correct maximum voltage, it does not go further than 3.29V which is exactly what we wanted.

Electronic CAD with EasyEDA